Research on Algorithms toward New Solver Systems Based on Discrete Optimization
Discrete optimization (or combinatorial optimization) forms one of the fundamental research fields in computer science, which has made the significant development due to the rapid growth of computer power and the recent progress on algorithm theory. It contains numerous problems that have been required to be solved in practical applications from many areas such as operation research, system science, bioinformatics, management, economics, social science and etc.
Mathematical modelling is used to formulate the real world problems to develop efficient and effective algorithms utilizing their mathematical structure. From the view point of discrete optimization, we carefully select important mathematical models that underlie numerous practical problems rather than separately formulating a specific model for each real world problem.
We conduct research for solving these models according to the following guideline.
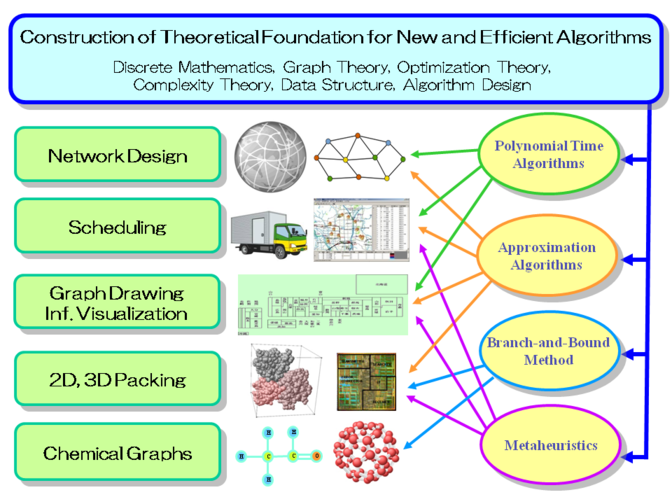
- Establishment of Theoretical Foundation: To design of new algorithms and data structure, we contribute to development of the theoretical foundation on optimization theory and complexity theory by applying the results in graph theory and discrete mathematics.
- Design and Analysis of Algorithms: For the fundamental problems in discrete optimization, we design new efficient algorithms under the algorithm frameworks suitably selected according to the complexity hardness, the size and type of problem instances, and required solution quality.
- Construction of Solver Systems: We formulate new mathematical models, and construct a solver system for each of the models by integrating related algorithms effectively so that any types of problem instances represented by the model can be solved efficiently and adaptively.
Currently we work on constructing new solver systems for graph drawing, 2D and 3D packing of irregular objects, and enumeration of chemical graphs.