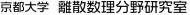グラフ・ネットワーク問題に対する理論研究
グラフやネットワークに関連して現れる最適化問題に対する理論は,現実に現れる様々な応用問題を解決するた めの基礎となります.私たちは,幅広いクラスの問題に対して,離散数学やアルゴリズム設計のテクニックなど を用いて,理論的な解析の研究を行っています.
問題の複雑さ
最適化問題には,多項式時間で解ける問題もあれば,多項式時間では解くことが不可能だと予想されている「難しい」問題(NP-困難問題,NP-完全問題)もあります.また多項式時間ではあっても,少ない計算量で解ける「たちの良い」問題から,多くの計算量を必要とする問題まであります.
たちの良い問題に対しては,アルゴリズムを提供することだけではなく,その問題の裏にどのような構造が隠れているかを数学的に解析することで,より深く問題を理解し,他の問題に対するアルゴリズム開発の糸口を与えることにつながることが期待できます。 また難しい問題に対しては,最適解ではなくて近似解を計算する近似アルゴリズムなどのアプローチがあります.この場合,計算量だけではなく,最適解にどれだけ近い近似解が求められるかを表す近似精度が,そのアルゴリズムの性能を計る指標となります.
私たちは,計算可能性や近似可能性の意味で「易しい」問題から「難しい」問題まで,グラフ理論や離散数学、データ構造やアルゴリズムなどの計算理論、線形計画などの最適化の理論などをツールとして,アルゴリズムの開発や問題構造の解析を行っています。
グラフの連結性に関する最適化問題
グラフの連結性とは,そのグラフの結びつきの強さを表す指標で,情報ネットワークの耐故障性や通信量などにも関係することから,情報基盤技術や社会経済活動に重要な役割を果たします.ネットワークフローやグラフのカット構造などと深く関係があり,グラフのスパース化,グラフ増大問題,ネットワーク設計問題、供給点配置問題など,世界的に研究が盛んです.私たちのグループは,これらの研究において最先端の成果を挙げています.
例えば,グラフの連結度を計算する最小カット問題に対しては従来、ネットワークフローに基づく反復アルゴリズムが使われていました。私たちのグループはこの問題に対して、ネットワークフローを用いずに,最大隣接順序というノードの順序づけを利用した高速なアルゴリズムを考案しました[1].また[2]では,巡回セールスマン問題が基本構造は次数指定と連結度要求から成るネットワーク設計問題であると考え,より一般化された問題に対する近似アルゴリズムを与えました.
グラフ描画
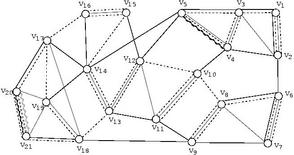
グラフを視覚化する際,平面や空間にいかに「きれい」に埋め込むかということが問題になります.「きれい」には様々な定義がありますが,例えば辺と辺が交差しないことであったり,一本の辺が折 れ曲がりの少ない線で描かれていたりという様々な要求が考えられています.私たちのグループでは,この方面でも活発に研究を行っています.
[3]では,各辺が平面上の水平もしくは垂直な線分で,かつそれぞれの内面が,指定した面積を持つ少ない角数の多角形になるようなグラフ描画アルゴリズムなどを開発しました.
彩色問題
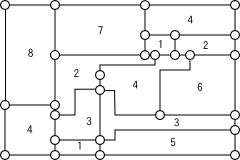
彩色問題では,グラフの節点をそれぞれ色で塗り分けることを考えます.そのとき,隣り合う節点を塗るには違う色を用いなければなりません.離散数学の世界で有名な四色定理では,平面グラフに対しては4色で充分であることが示されています.一般のグラフでは何色で十分かを求める問題はNP-完全であり,よい近似保証をもつ近似アルゴリズムを与えることも難しいとされている一方,パーフェクトグラフと呼ばれるクラスに対しては,多項式時間アルゴリズムが与えられています.
私たちは,彩色に用いる色数最小化を一般化したコスト関数として,一つの色で塗られる節点数の大きさに応じてその色にかかるコストが変化する関数を定義しました.さらに,このコスト関数をもつ最小化問題に対して,近似アルゴリズムを開発しました[4].
[1] H. Nagamochi, T. Ibaraki, Computing the edge-connectivity of multigraphs and capacitated graphs,
SIAM Journal of Discrete Mathematics, 5, 1992, pp.54-66.
[2] Takuro Fukunaga, Hiroshi Nagamochi, Network design with edge-connectivity and degree constraints,
Proc. 4th Workshop on Approximation and Online Algorithms, LNCS 4368, 2006, 188-201.
[3] A. Kawaguchi, H. Nagamochi,Orthogonal drawings for plane graphs with specified face areas,
Proc. the 4th Annual Conference on Theory and Applications of Models of Computation, LNCS 4484, 2007, 584-594.
[4] T. Fukunaga, M. Halldorsson, H. Nagamochi, Robust cost colorings,
Proc. ACM-SIAM Symposium on Discrete Mathematics 2008.