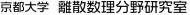詰め込み問題に対する実用的なアルゴリズムの開発

詰め込み問題とは, 与えられた図形を容器の中に図形の重複がないように配置する問題です. 図形の種類, 配置の制約, 容器の形状などにより様々なバリエーションがあり. 広く応用のある重要な問題です. 私たちは詰め込み問題に対する汎用的なフレームワークの構築を目指しています.

詰め込み問題

詰め込み問題は, 与えられた図形を容器の中に図形の重複がないように配置する問題です. 例えば、以下のような問題を含んでおり, 非常に多くの応用があります.

ただし, 一般的に詰め込み問題は多項式時間で解くことができないと予想されている「難しい」問題です. そこで, 私たちはこの問題に対して, 広く応用が効くような汎用的な解法の開発を目指しています. 問題が比較的易しい場合には, 最適な解を実用的な時間で求める厳密解法の研究を, 規模の大きい問題や難しい問題に対しては, 高速に実用的な解を見つけるような発見的手法の研究を行っています. 以下に, この研究室で取り組んでいる問題を個別に紹介します.

長方形の詰め込み問題

fig1

長方形を長方形の容器に配置する問題は, 鉄板を材料とする産業などに応用のある問題です. 私たちは, 幅が固定された容器の中に, 与えられた長方形を配置する際に, 必要となる容器の長さを最小化する問題に対する厳密解法を提案しています[1]. 実際の応用上では, 長方形の配置の様式に従うことが求められることがあります. その代表的な例として, ギロチンカット制約と2ステージ制約が挙げられます. ギロチンカット制約とは, 容器の長方形を端から端まで切り取ることを繰り返すことで, 与えられた長方形が切り出せるような配置になっているという制約で, 2ステージ制約は, ギロチンカット制約の特殊な場合です. 配置の様式の他にも, 長方形間のハミング距離が最小となるような配置を求める問題に対する研究も進めています. これは, VLSIの設計で, モジュール間の配線の総距離を短くする問題などへの応用があります.

fig2

非凸多角形の詰め込み問題

非凸多角形を幅が固定の容器に配置する際に必要になる容器の長さを最小化する問題に対する発見的手法を提案しています[2]. この問題は繊維産業や家具産業などに応用のある問題です. 例えば, 服の型紙をうまく配置することで, 服を作るのに必要となる布の量を減らすことがあります. 図形の回転は90度回転や180回転などの, 固定角度の回転を考慮に入れています. 図は水着の型紙の配置を[2]のアルゴリズムで計算したものです.

Multi-sphere Scheme

図形の回転には, 任意の回転角を許す自由回転というものがあります. 従来, 図形の自由回転を許す詰め込み問題は困難だと考えられてきました. 私たちは, 図形を二次元なら円, 三次元なら球の集合で近似することで, 任意の図形の自由回転を許した状態で重複のない配置を求めるというスキームを提案しています[3]. もちろん回転を許さない場合も扱うことができます.

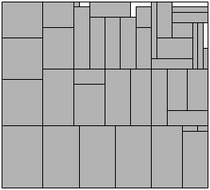
ラベルの再配置問題とは, 与えられたラベルの配置において, いくつかのラベル同士が重複している場合に, その重複を取り除くように, ラベルを再配置させるという問題です. 再配置の際には, 元の配置からあまり変化しないことを考慮に入れる必要があります. この問題は可視化における重要な操作です. 私たちは, multi-sphere schemeの中の局所的なアルゴリズムを適用することで, 元の配置からあまり変化させずにラベルを再配置させることに成功しました. 下の図は, 東京の鉄道の駅の位置に長方形のラベルを置き, 再配置させた結果です.

fig3

タンパク質の詰め込み問題とは, タンパク質の分子を球集合で表し, それぞれのタンパク質が剛体であるという仮定の下で, 容器の中に詰め込む問題です. 下の図は, 複数のタンパク質を立方体の容器に配置した結果です. この問題は, 生物情報学で重要なタンパク質のドッキングの特殊な場合になっています. 将来的には, ドッキング問題を扱えるようにスキームを拡張していく予定です.

fig4

2009年京都大学情報学エデュテインメントの支援をうけて，このパッキングソルバーのGUIインターフェィスを作りました．ソルバーの詳細を知らない人でも比較的に簡単に問題を解いたり，結果を確認したりできるようになりました．もっと知りたい方は，サンプル入力（X3Dファイル）とそれに対する出力ファイル（X3Dファイル，動画形式）をご利用下さい．これらのX3Dファイルは，例えばOctaga Playerなどで再生できます．実行画面は以下のようになります．入力は，三角形の面で表している三つの物体をそれぞれ異なる色の球で近似して適当な初期配置に置いておいた状態を示しています．出力は，物体がお互いに重ならないようにコンパクトにドッキングしている様子を示しています．なおX3Dファイルでは三次元の構造になっており，様々な角度や距離から見ることができます．さらに出力ファイルは計算途中の様子も示しています．

fig5

fig6

NEW! 別の実行例です．りんご八個をパッキングしている様子を示しています．このファイルはそれのX3Dファイルです．マウスでクリックすると再生されます．

fig7

[1] M. Kenmochi, T. Imamichi, K. Nonobe, M. Yagiura, H. Nagamochi : Exact algorithms for the 2-dimensional strip packing problem with and without rotations, European Journal of Operational Research, 198(1): 73-83 (2009).
[2] T. Imamichi, M. Yagiura, H. Nagamochi : An iterated local search algorithm based on nonlinear programming for the irregular strip packing problem, Discrete Optimization, vol. 6, no. 4, pp. 345-361, November 2009.
[3] T. Imamichi, H. Nagamochi, A multi-sphere scheme for 2D and 3D packing problems, LNCS 4638, 2007, 207-211.