＜グローバーのアルゴリズムについて＞
これは特定の状態の確率振幅を増幅するアルゴリズムです。 例えば SAT の問題に応用できます。
n 変数の SAT は 2 の n 乗の解の候補がありますが、 それを重ね合わせてそれぞれ充足するかどうか実際に計算します。 そして充足する候補だけの振幅を増幅してそれを観測するようにするのがこのアルゴリズムです。
古典的にはN 個の候補から一つを選び出すには O(N) の計算量がかかりますが このグローバーのアルゴリズムによると O(√N) の計算量できます。

＜このデモについて＞

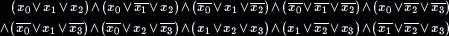
という４変数１０クローズの SAT の問題を、以下の手順で解きます。 x軸の 0 は x₀=0, x₁=0, x₂=0, x₃=0 に対応し、 充足する解の 3 (x₀=1, x₁=1, x₂=0, x₃=0) の振幅が大きくなっていきます。 √１６ より小さい３ステップで計算が終了します。

Step (n)-1

正しい解の振幅にマイナスをかける。

Step (n)-2

Walsh-Hadamard （ウォルシュアダマール）変換をかける。 これは４個のビットすべてに という２×２ユニタリ行列をかける操作です。

Step (n)-3

0の振幅にマイナスをかける。

Step (n)-4

Walsh-Hadamard 変換をかける。

Step (n)-5

すべての振幅にマイナスをかける。